













































































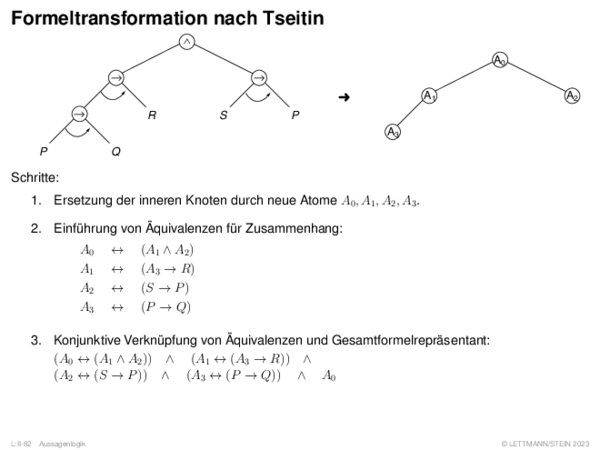
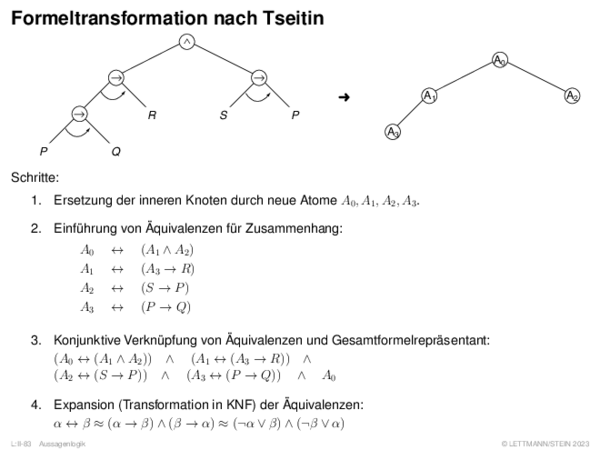






















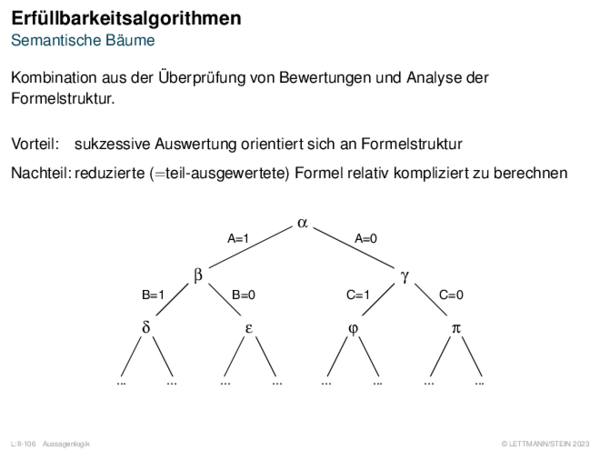




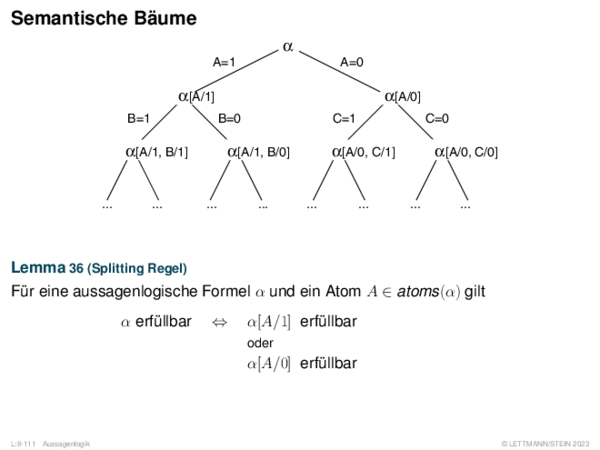



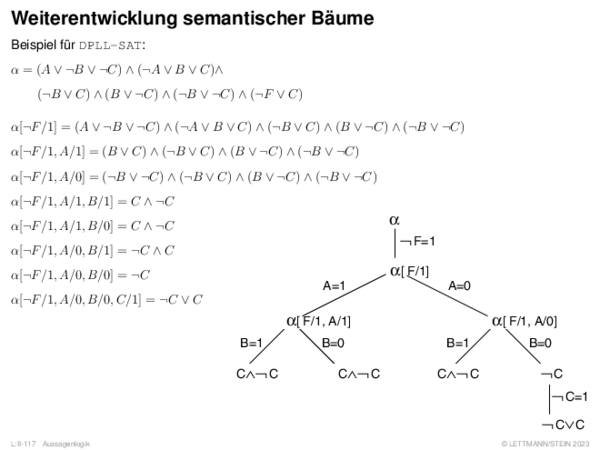
![Weiterentwicklung semantischer Bäume Verallgemeinerung von α[A/1].](https://downloads.webis.de/lecturenotes/logics/unit-de-propositional-sat-semantical/unit-de-propositional-sat-semantical-20.png)
![Weiterentwicklung semantischer Bäume Davis-Putnam-Algorithmus [Davis/Putnam 1960, Davis/Loveland/Logemann 1962]](https://downloads.webis.de/lecturenotes/logics/unit-de-propositional-sat-semantical/unit-de-propositional-sat-semantical-21.png)
































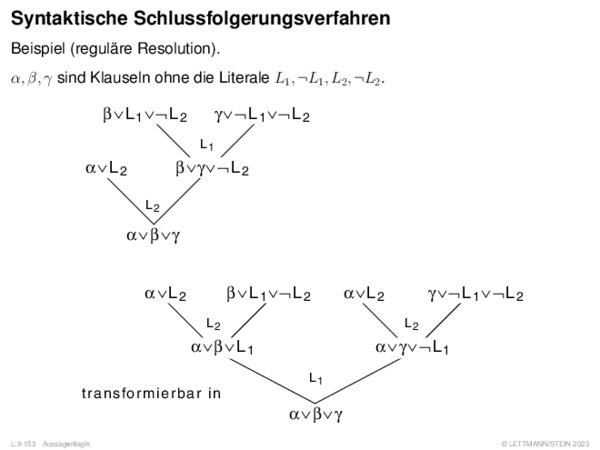

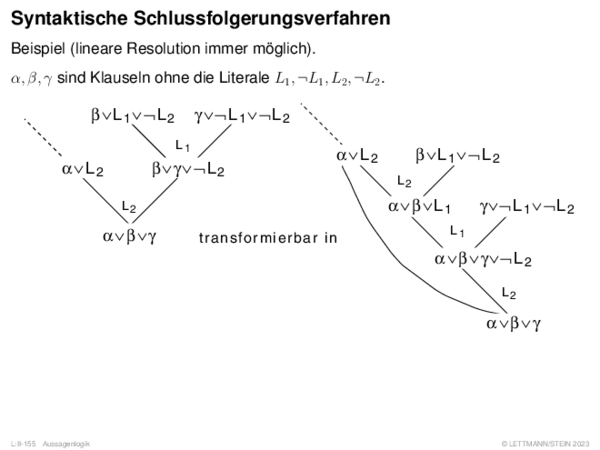























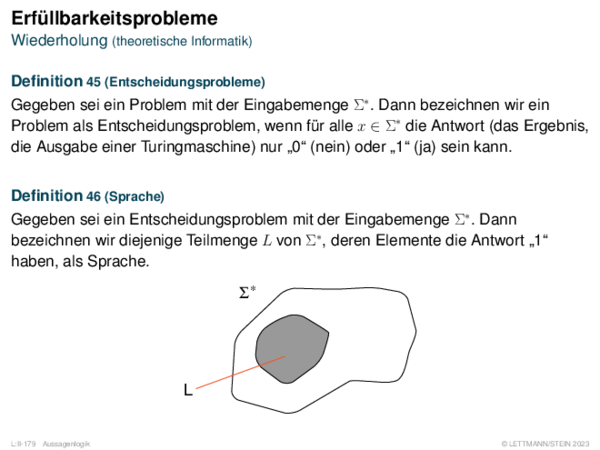


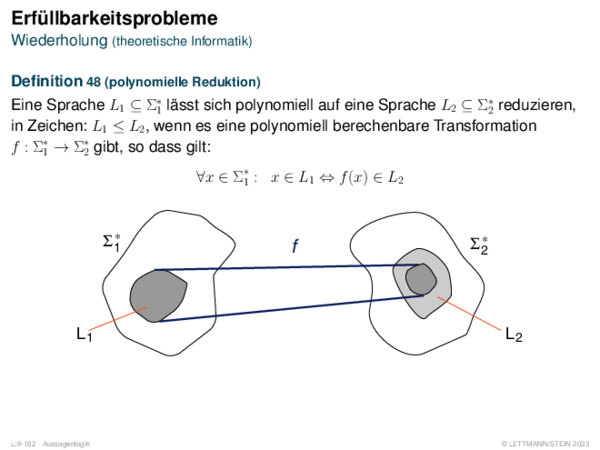





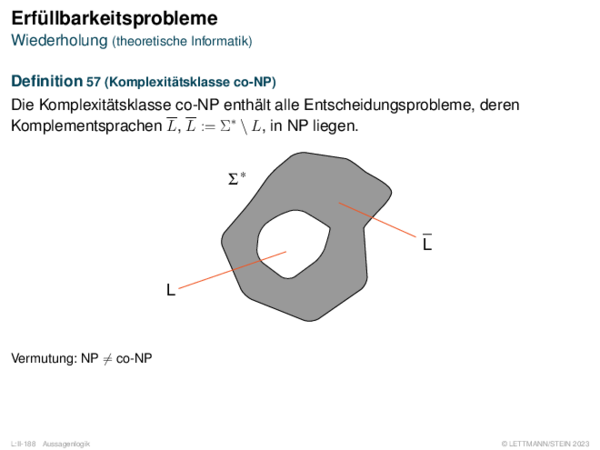





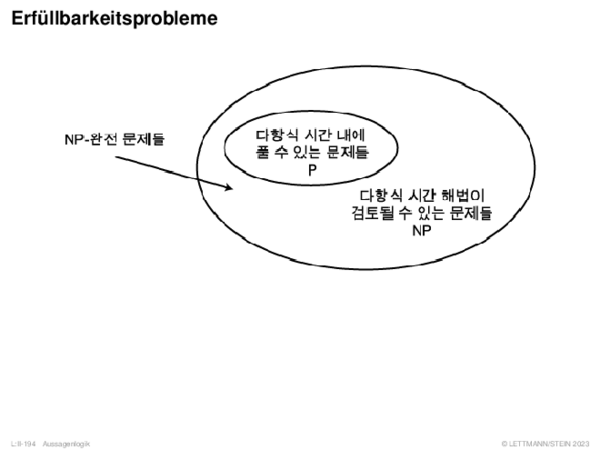

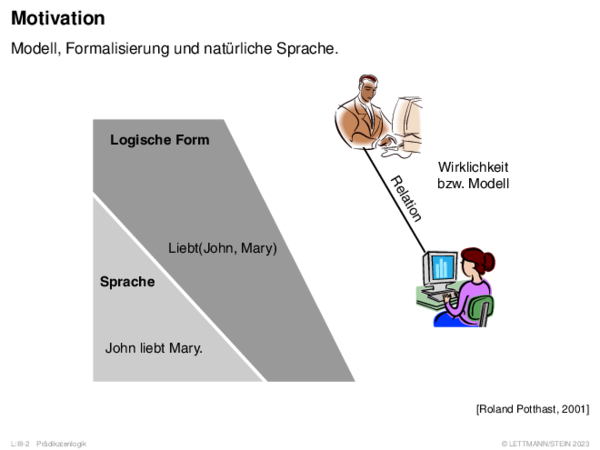
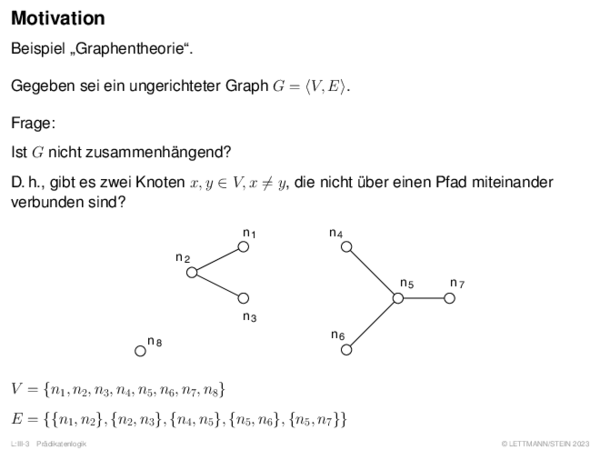



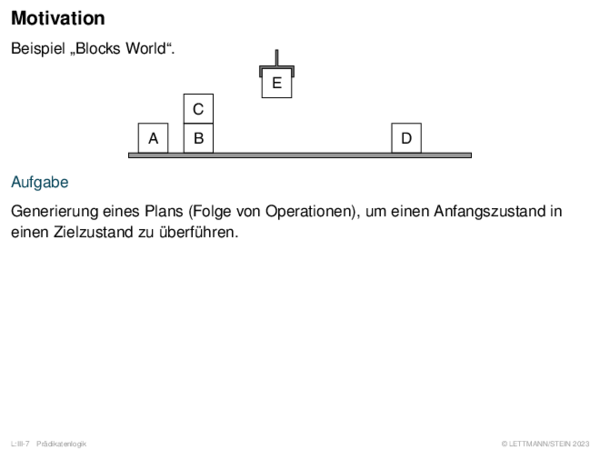




























































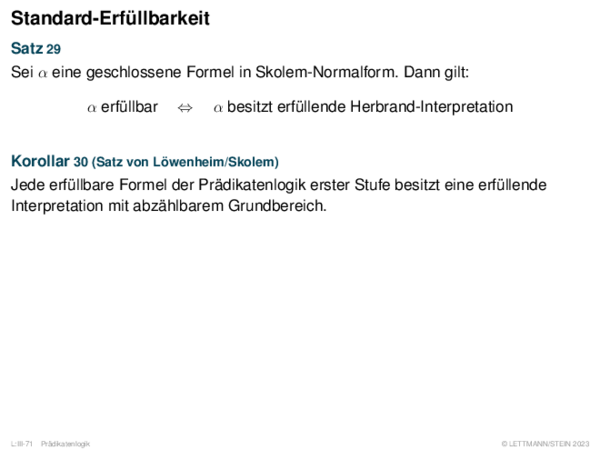








































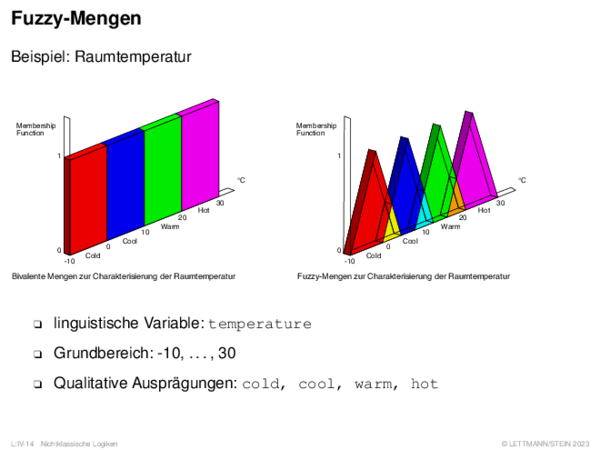



















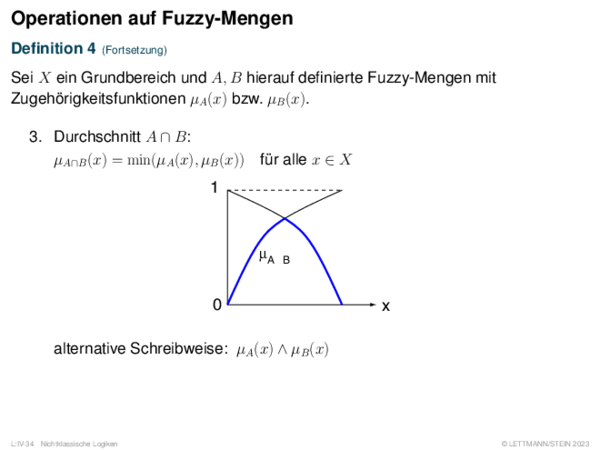
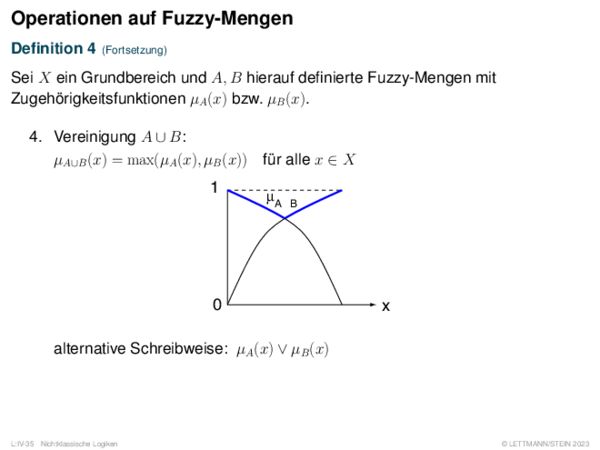
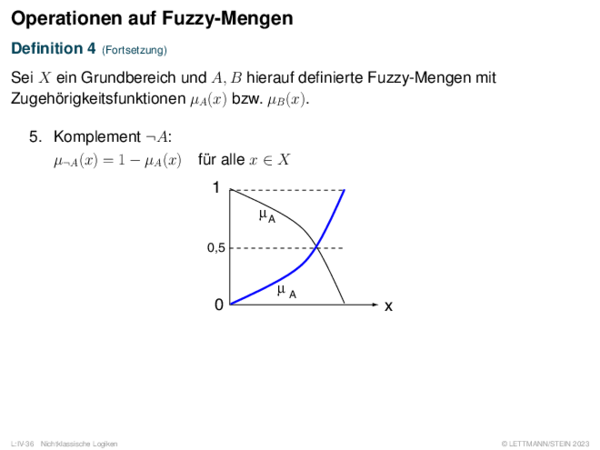



















![Fuzzy-Inferenz Max-Min-Inferenz[Mamdani 1977]](https://downloads.webis.de/lecturenotes/logics/unit-de-fuzzy-inference/unit-de-fuzzy-inference-9.png)


























































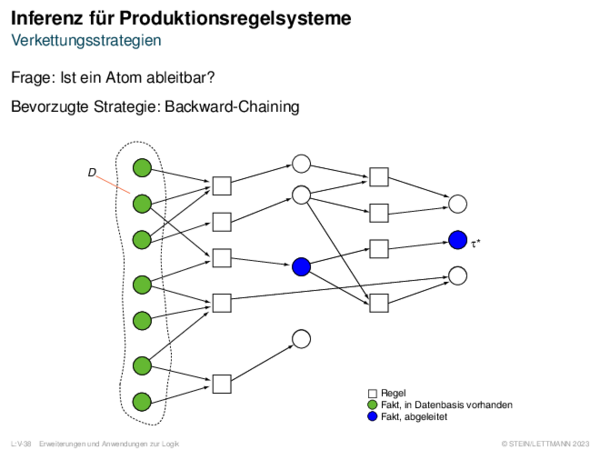
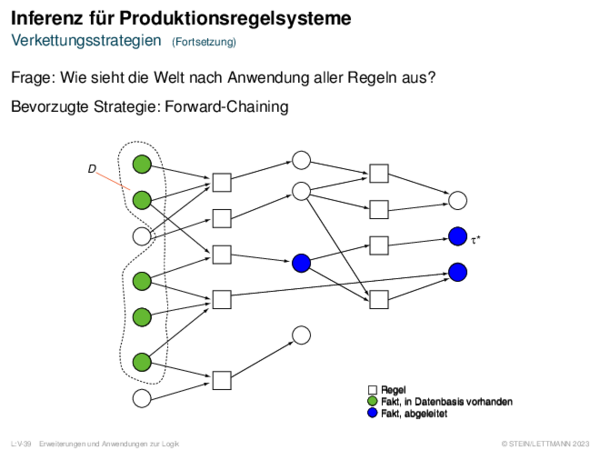















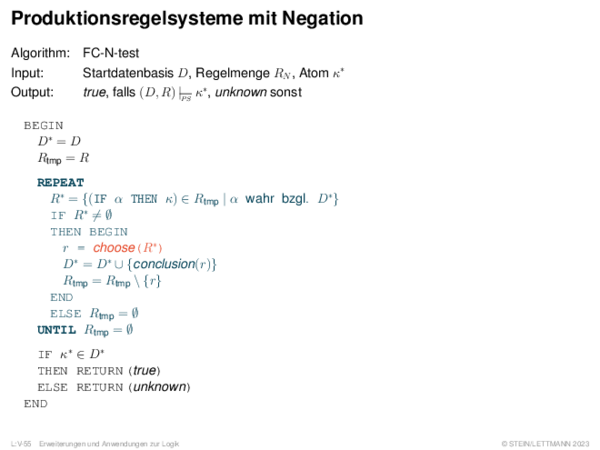














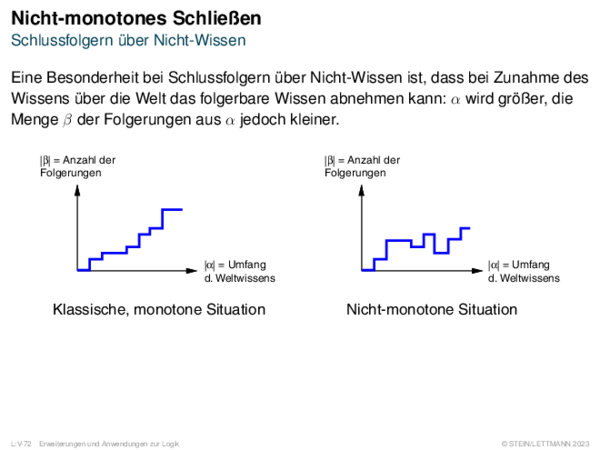
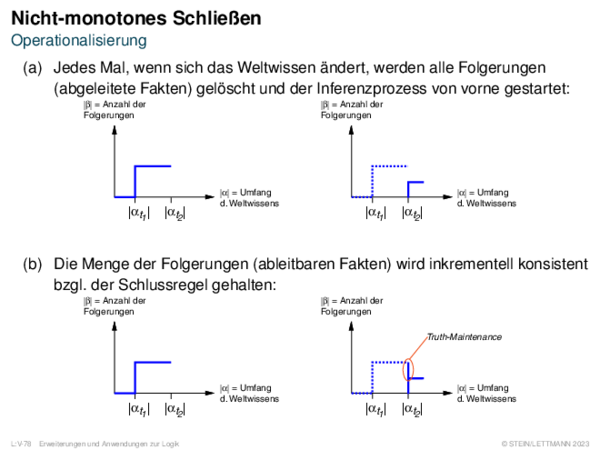
![Nicht-monotones Schließen Schlussfolgern über Nicht-Wissen: Default-Logik [Doyle/McDermott 1980]](https://downloads.webis.de/lecturenotes/logics/unit-de-non-monotonicity/unit-de-non-monotonicity-10.png)








































































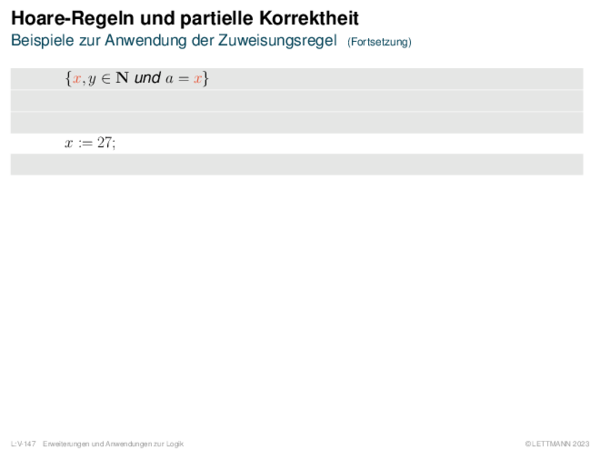
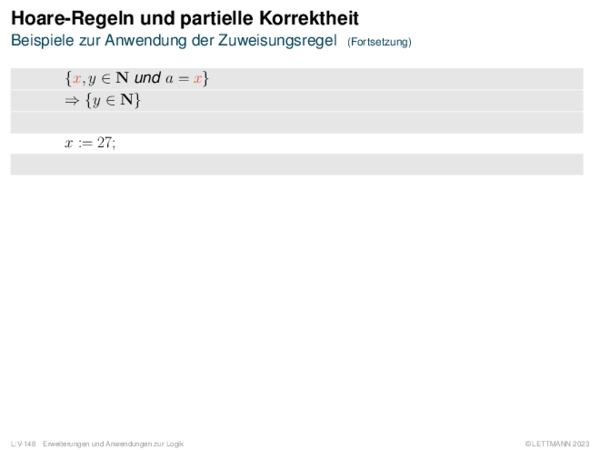
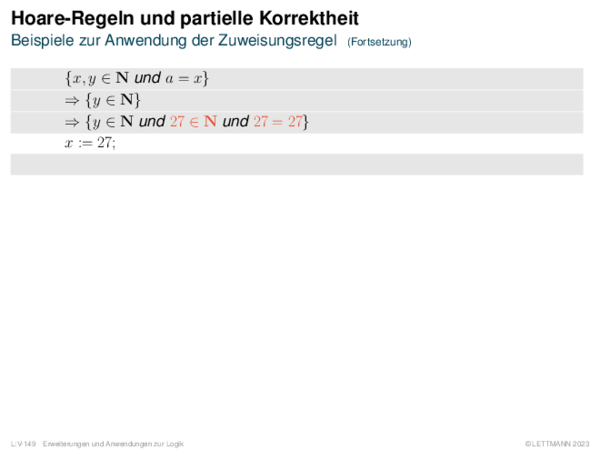







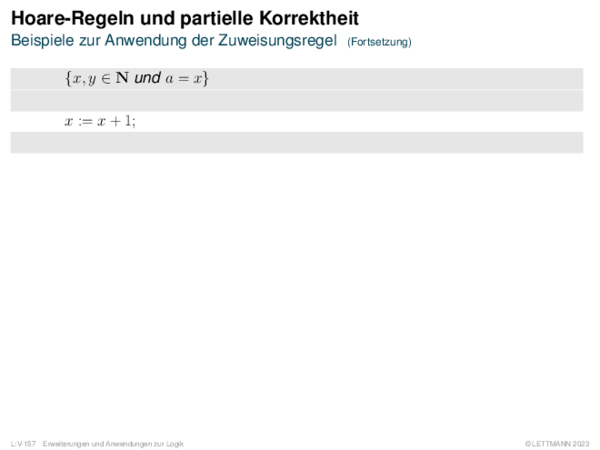




















































































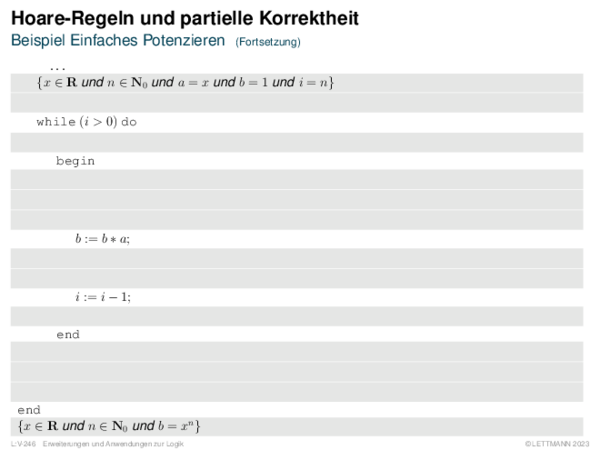





















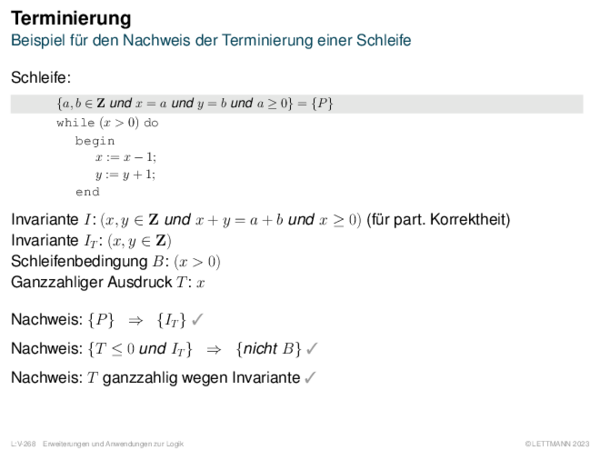

















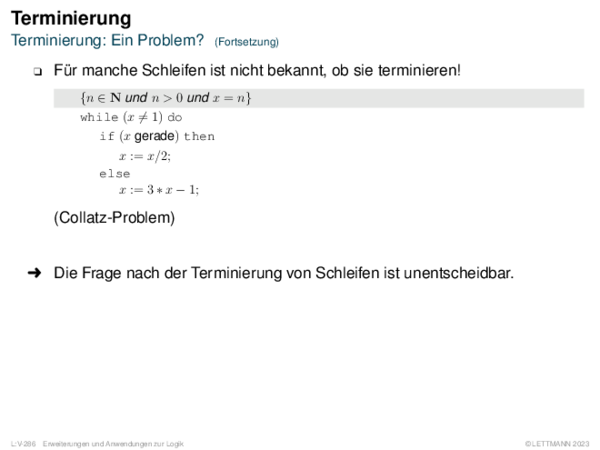
































































































































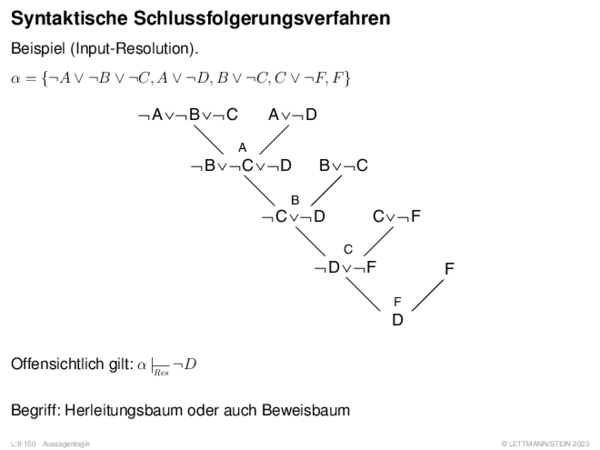
![Weiterentwicklung semantischer Bäume Verallgemeinerung von α[A/1].](https://downloads.webis.de/lecturenotes/logics/unit-de-propositional-sat-semantical/unit-de-propositional-sat-semantical-20.png)
![Weiterentwicklung semantischer Bäume Davis-Putnam-Algorithmus [Davis/Putnam 1960, Davis/Loveland/Logemann 1962]](https://downloads.webis.de/lecturenotes/logics/unit-de-propositional-sat-semantical/unit-de-propositional-sat-semantical-21.png)




















































































































































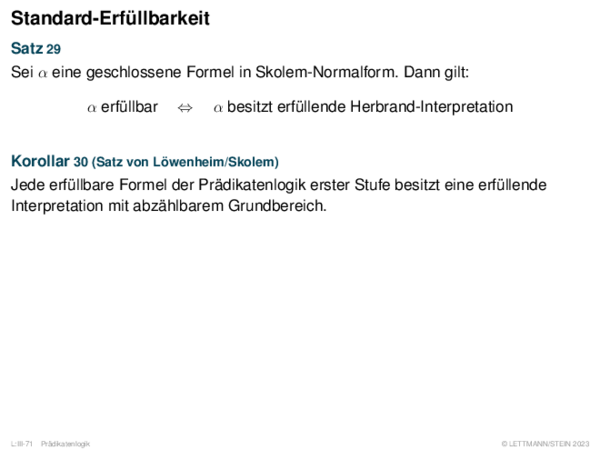


















































































![Fuzzy-Inferenz Max-Min-Inferenz[Mamdani 1977]](https://downloads.webis.de/lecturenotes/logics/unit-de-fuzzy-inference/unit-de-fuzzy-inference-9.png)

























































































![Nicht-monotones Schließen Schlussfolgern über Nicht-Wissen: Default-Logik [Doyle/McDermott 1980]](https://downloads.webis.de/lecturenotes/logics/unit-de-non-monotonicity/unit-de-non-monotonicity-10.png)

































































































































































































































| Shortcut | Documents |
|---|---|
|
↑/↓
|
Navigate documents |
|
Shift + ↑/↓
|
Navigate 3 documents |
| Shortcut | Pages |
|---|---|
|
←/→
|
Navigate pages |
|
Shift + MouseWheel
|
Navigate pages |
|
Shift + ←/→
|
Navigate 3 pages |